简单总结蓝皮书第12章的核心内容,只写要点,下次快速反刍。部分内容来自公司的SPC培训资料。
主要内容:控制图理论(为什么),两类响应变量(计数型,计量型),计量控制图,计数控制图,特殊控制图(略),非正规条件的控制图(略),过程能力分析。
我重点学习的内容:控制图理论、两类变量类型及其控制图,过程能力分析
控制图理论
SPC 的目的,特殊因素和随机因素,8个判异准则,SPC的两个阶段
Q:为什么要做SPC?
通过监控过程变量,提前预判产品波动是否正常,都是随机因素的影响,还是存在特殊因素(比如设备出现破损等)。
接受随机因素,识别特殊因素并及时纠正,避免生产大量的残次品,做好预防工作。
随机因素:温度波动,原料波动,测试波动,等
特殊因素:比如生产时,设备内部出现未识别的故障,或工艺出现了某个修改,都可以从SPC来预警。
- All processes have variation in them, it is the noise in the process. 所有的过程都包含变异,变异是一个过程的不好变化。
- There are two types variation 变异产生的原因有两种
- Common Cause 普通原因(非机遇性原因)
- Special Cause 特殊原因(机遇性原因)
Q:为什么是六西格玛(平均值加减三个西格玛),不是三西格玛,或十西格玛?
答案:我们接受多大的产品质量波动,或者过程不合格率,比如要求99%合格,还是99.9%合格,抑或更严格?根据正态分布的“68-95-99.7”规则可知,有99.7%的概率,过程响应变量落在平均值加减三个西格玛的范围内!!所以我们把99.7%视为“识别特殊波动”的分水岭。
Q:异常点是什么?七个判异原则(run rules),如何证明“过程变异由特殊因素造成”。
答案:异常点的定义,对应于第一条判异原则,即落在界限(平均值加减三个西格玛)之外的数据点,可判定为异常点,因为抽样99.7%的概率落在控制限以内!!
数据点落在控制限以外,肯定是异常点!但所有的数据都落在控制限以内,并不代表不存在异常! 这就是“七个判异原则”的价值。这具体的七条判异原则,也就是七个检测清单(Checklist),用来方便判断“系统出现了特殊因素,需要纠正”。
- Run rules tell us when to act. •判异准则告诉我们何时采取措施
- Run rules have been developed to help the user interpret the data to ensure that a special cause issue is not confused with a common cause issue. •判异准则用来帮助控制图的使用者解释数据以确保普通原因和特殊原因不被混淆

| 1 | Beyond Limits | One or more points beyond the control limits 1个或多个数据点超控制限 |
| 2 | Zone A | 2 out of 3 consecutive points in Zone A or beyond 连续3个点中的2个点落在A区或超出A区 |
| 3 | Zone B | 4 out of 5 consecutive points in Zone B or beyond 连续5个点中的4个点在落B区或超出B区 |
| 4 | Zone C | 7 or more consecutive points on one side of the mean (in Zone C or beyond) 7个以上连续点在均值的一边(落在C区或超出C区) |
| 5 | Trend | 7 consecutive points trending up or trending down 连续7点递增或递减 |
| 6 | Mixture | 8 consecutive points with no points in Zone C 连续8个点都没有在C区内的 |
| 7 | Stratification | 15 consecutive points in Zone C 连续15点落在中心线两侧的C区内 |
| 8 | Over-control | 14 consecutive points alternating up and down 连续14个点相邻点交替上下 |
这八个判异原则,看起来简单,背后都是概率!有些看起来甚至会违背直觉,比如原则7——连续15个点都在更窄的范围(average+-一个西格玛)内波动,这难道不是系统控制得更好的表现吗? 再比如原则5和8,”过度整齐的规律性”。
统计学上可以证明,以上8种现象出现的概率大体都等于或接近0.27%(1-99.7%),小概率事件的发生导致我们判定过程为异常。——《六西格玛管理统计指南》蓝皮书
控制图的类型
数据分成两类:连续型(计量)和离散型(计数),这两类数据对应两大类控制图,即计量型控制图和计数型控制图。
连续型响应变量:温度,压力,硬度,pH,等等(连续变化的变量)
离散型响应变量:合格品数量(不会超过总检测数量)及其转化的合格品率,缺陷数量(一个产品上可能有多个缺陷)及其平均缺陷数。
常用的计量控制图,有单值-移动极差图(I-MR图),均值-极差图(Xbar-R图),均值-标准差图(Xbar-S图)。
常用的计数控制图,有不合格品率图(P图),不合格品数图(NP图),单位产品缺陷数图(U图),和缺陷数图(C图)。
具体的计量控制图,如何计算,此处略,具体见P424,注意几个问题:
- 为什么计量控制图至少需要两张图?——同时关注Center和Spread!
2. 对于计量控制图,如何计算收集的数据的均值和极差(Range, 又称“全距”,最大值与最小值的差值)?如何计算均值和极差各自的上下限(关键是两个标准差的计算)?
3. 对于计数控制图,分为计件型和记点型,各自的控制限的计算公式——P429
问题:实际工作中,如何设置控制限?如何设定具体的上下限位置?
答案:根据以往收集的数据,计算以往数据的center,spread和各种统计描述量,然后基于此,确定平均值和波动性(均值可能和产品设计有关,而波动的标准差,更多来自以往采集数据的分析)。
Control limits are the historical variation of the process / 控制限的设置要依据过程的历史变化。
国标规定,制定分析控制图时,在合理分组的前提下,至少要采集25组数据,用来计算控制限。 P425
过程能力分析(Process Capacity Analysis)
这是本章最重要的一部分内容,之前的部分属于“定性分析”,通过控制图分析过程是否稳定受控,是否存在异常值,如果存在异常值,就要分析可能的特殊变量(比如工艺除了某个改变)。
通过“过程能力分析”进行“定量判断”,进一步确认过程能力是否达到顾客的要求。
全面定量分析还是看两个方面,一是波动大小,二是偏倚大小。都要对应的定量描述参数。
Cp,Cpk反映的是短期内过程输出满足产品质量要求的程度,Pp,Ppk则是反映过程长期的总波动满足质量要求的程度。
几个问题,还需要重读分析:
- 如何计算过程能力指数(Cp,Cpk)和过程绩效指数(Pp,和Ppk) (“k”是日语“片寄り(katayori)”的首字母,意为偏倚)
- 如何根据以上数值的关系,判断波动大小、偏倚大小。
- Cp和Cpk的关系及其含义,
传统来看,Cp>1是可以接受的过程能力。从六西格玛角度看,Cp>2(公差超过12个sigma)才算理想的过程。 - Pp和Ppk的关系及其含义
- 如何评估长期和短期能力?
这一部分读的还比较粗略,等实战时再研究吧。
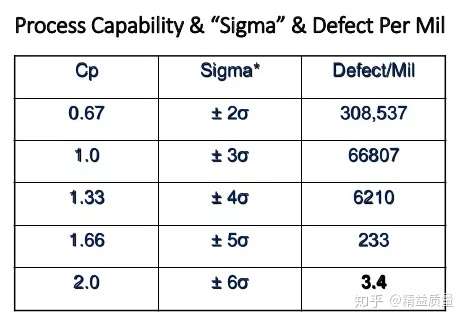
下表展示了过程能力指数,西格玛水平和百万不良数之间的关系。
2020.8 早晨读书,这一部分只算学了个皮毛,懂了原理,严重缺乏实践。