书名:《试验设计方法与Design-Expert软件应用》
主编:葛宜元
第一章 试验设计基础知识
- 20世纪20年代(100年了),Fisher在《研究工作者的统计方法》一书中提出“试验设计”的概念和方差分析方法!
- (科研基本工具)良好的试验设计可以最大限度地排除各种非试验因素的干扰,提高科学实验的效率和精确度。一次良好的试验设计就等于试验成功了一半!
- 试验设计的几个主要内容(DOE的基础步骤,Design expert handbook中也有如下内容,只不过写的更详细)
- 确定指标,即response(响应变量)
- 寻找影响因素,即factor,根据专业经验确定水平和研究范围
- 选择合适的试验设计方法(筛选,优化,RSM;稳健等)(序贯试验,迭代实验!)
- (善用统计软件)科学地分析试验结果,包括直观分析(看图),方差分析(看波动),回归分析等多种统计分析方法。
- 一个良好的试验方案,不仅需要具备概率论与数理统计的知识,还需要有宽广的专业知识和丰富的实践经验,三者结合,才能取得理想的结果。(方法论+专业知识+经验)
- 试验设计的目的
- 合理安排试验,减少试验次数
- 量化影响因素的主次关系(根据方差分析的F值),抓住主要矛盾!
- 确定模型(近似函数关系),进行预测和优化
- 因素之间的交互作用(量化而不是主观分析)
- 找出较优的参数组合,确定试验方向。
- 试验设计的三大原则:随机化、重复性和区组化(局部控制)
- 常用数学模型
- 方差分析模型 —— 分析因子、因素、模型系数等的显著性并进行大小排序
- 回归模型——确定模型中的各个系数,与方差分析相比,回归模型需要更多的水平,不然看Fit 没有意义 2023-3-26
- 非参数回归模型
第二章 Design Expert软件 (重看原文)
软件的功能模块:design,analysis,optimization
- design:对设计者的试验方案做出总结,对设计方案的好坏做出评估。
- analysis:方差分析,回归分析,(transform转换,effects排列,anova,diagnostics,model graphs)
- optimization:预测最优值,给出最优试验条件以便验证
软件提供四大类试验设计:组合设计combined,析因设计factorial,响应曲面设计RSM,混料设计mixture
问题:何时用combined design,何时将combined分成独立的factorial和mixture?如果一个DOE本来可以用mixture,却实际使用了combined design,会有什么影响?
组合设计combined design
析因设计:
- 一般因子设计General factorial (单因子多水平的方差分析,两因子不重复试验,两因子等重复实验,这些都是用general factorial,重要的是正交化。)
- 2水平析因设计:(最经典的DOE,只看两个水平,不考虑弯曲性,最后会区分出主效应和交互作用;如果忽略三阶及以上的交互作用,就可以做部分析因设计fractional factorial design(分式析因设计);常用于筛选试验,暂时不需要看响应曲面(先用两水平实验设计,缩小factor范围和数量)
- 筛选试验设计PB:因子多,未确定因子的显著性,不能区分主效应和交互作用;
- 田口Taguchi设计
响应曲面设计:(暂略)【析因设计的中心点实验可以判断模型是否存在弯曲,使用RSM研究弯曲的实验设计,即非线性影响,需要更多的实验点,一般是序贯设计,增加轴点等)
问题:大家常用析因设计,做几个中心点实验,就生成模型,这样和完整的RSM实验相比有什么问题吗?
备注:RSM一般是通过序贯实验获得,先做最简单的析因设计,然后根据情况增加实验点,做做RSM分析;一般一步就做到RSM,可能会有问题,比如一开始聚焦的范围太大或太小;而RSM的核心是,先用析因设计找大范围,再用RSM对局部进行详细研究。
- CCD中心复合试验设计
- B-B设计
混料设计: (暂略)
第三章 方差分析
Fisher最先提出方差分析方法,所以方差分析又叫F检验。
Q:何时进行方差分析(F检验)?
A:统计结果包括平均值和标准差;要想比较两个条件下的结果是否一致,除了看均值差,还要看波动。而波动大小的量化,就是方差分析法。
备注:之前minitab的一篇博文,某一款食物的某一种原料被替换之后,进行消费者评估,得到两组数据,分析均值差是否具有显著性,以判断消费者是否能察觉到差异。见DOE篇:配对t检验的一个应用举例。
方差分析的前提:独立性、随机性和方差齐性
方差分析的目的:在满足三个前提的情况下,分析各处理组之间的均值差异,以判断总体均值之间的差异,从而说明处理因素(factor)之间是否有不同(显著,非常显著,不显著)。
软件方法:
3.1 单因素方差分析
相当于DOE中的单因子多水平试验,比如某一个因子设定了五个不同的水平,分析这五个水平之间是否有显著性差异,当然每个水平下都要进行随机重复试验,以降低单次测试的误差。
P38 机理解释:(细读原文)
- 数据的总波动包括误差error,和改变因子产生的波动。
- 离差平方和分解公式: 数据总的离差平方和=因素水平改变引起的离差平方和 + 误差离差平方和。 (三个分别怎么计算要清楚)
- 自由度:
- 最后利用平方和分解公式、自由度,进行F检验!
- P41 方差分析表,如下图所示,通过F检验,判断单因素A水平的改变对响应y是否有显著影响。(零假设)


多重比较(S检验)(P42 跳过未细读)
使用Design Expert 12进行单因素方差分析研究:factorial design – randomized – multilevels categoric, 输入factor,每个有几个level,重复次数,输入response,填写测试结果,方差分析即可。为什么是categoric,因为方差分析只是告诉我们不同水平之间是否有显著性差异,并不会建立回归方差(针对numeric factor),所以方差分析中都直接用categoric即可。——2023-4-5
3.2 两因素不重复试验方差分析
不重复试验,每个条件(因子+水平)只有一个数据,这样就不像后面的“等重复”试验需要计算平均值了。
两个因子多个水平,两两组合,给出每个组合下的一次实验结果,有点像“列联表”。
只能给出有无显著性,不能确定是哪两个。
在design expert中,两因子多水平,使用factorial design- factorial design – general design,分别输入两个因子及其对应的多个水平。
3.3 两因素等重复试验方差分析
相比于3.2,这儿多了一个重复试验,所以每个条件下就有多个结果,计算平均,方差计算相似。只不过多了重复试验,这样就可以计算曲率。
总之,方差分析,完全可以用design expert软件实现。
第三章方差分析 练习题
例3.1
方法:factorial — Randomized — multilevel categoric

输入response,不知道信噪比,所以默认就不动了,软件提醒功效不足。


直观对比如下,可惜软件不能给出箱线图。

分析结果如下:
- 因为只有两个level,没有中心点,所以out of fit算不出来,
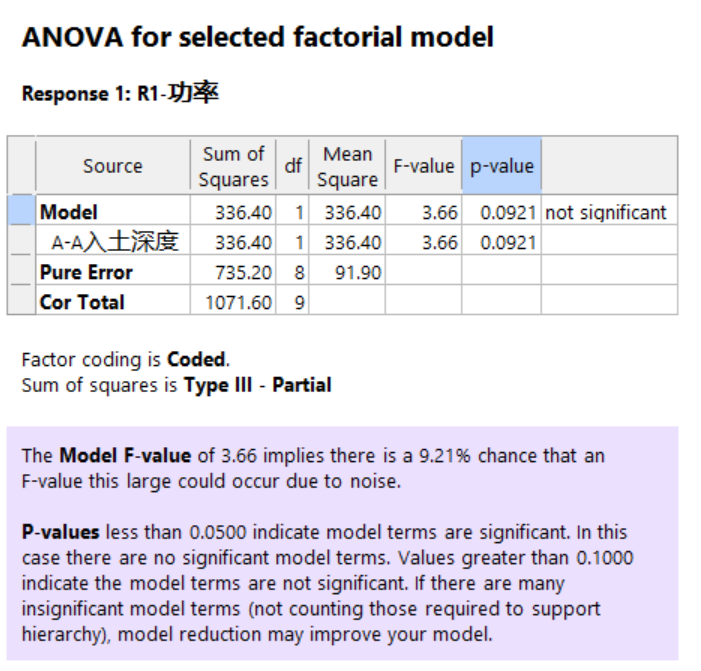
- 方差分析,书中给出的结论是,入土深度对功率的消耗,在alpha=0.1水平下显著。
- 软件直接给出了显著的置信水平0.092,即有9.2%的概率,入土深度20cm和30cm的差异是由噪声引起的。
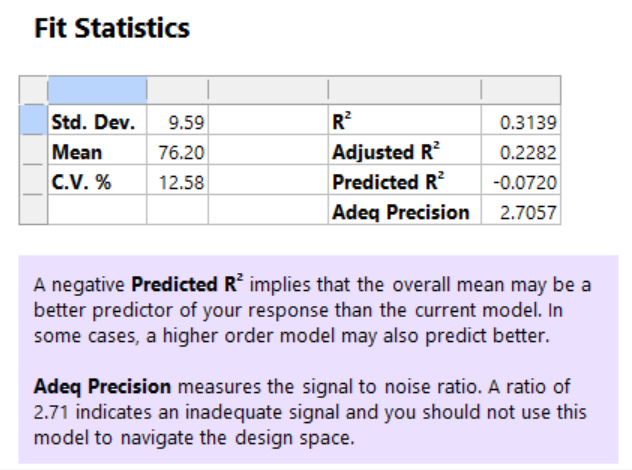
- 关于Fit statistics的R2很小的问题:这个例子只有一个因子两个水平,只是做水平之间的对比,本身不需要用模型,从上面的graphic也能看出来,两个水平的数据的分布很宽;所以Fit差是合理的。 ——2023-3-26
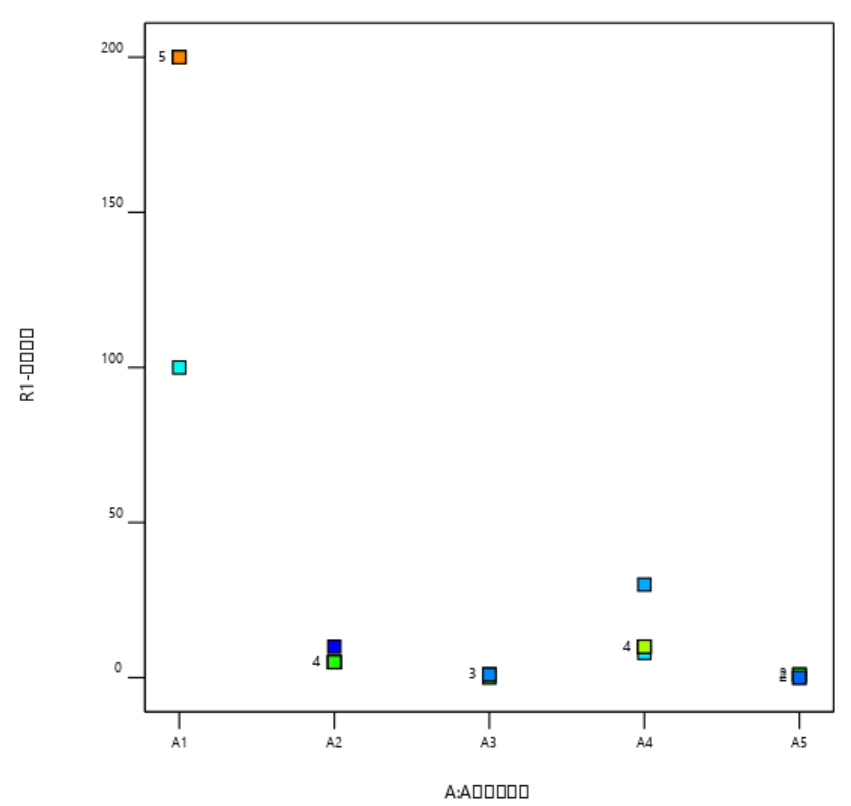
例3.2 五种硅酸盐地层的化学成分,是否有显著性差异
先查看graph Columns有一个直观的判断,A1明显和其他不同;方差分析F=82, p<0.0001,说明硅酸盐地层之间存在显著性差异; 根据treatment contrast判断水平之间是否有显著性差异。

2022-9-25
2022-9-26 done,第二三章还要再过一遍原文。
2022-9-27 晚上,再过一遍,更新
2023-4-5 更新书中的例子。