在科学和工程学领域,试验设计是改进产品和流程的非常重要的手段。但要用好DoE,首先需要掌握基本的DoE术语,“统一语言体系”,明确核心术语及其概念。
本文逐一介绍以下基本术语:
- 试验
- 试验单元、处理
- 响应、因子、水平
- 主效应、交互作用
- 模型、随机误差
试验
“试验设计”还是“实验设计”,各有道理,我倾向于前者,以强调探索和工程应用导向。但我会保留引用文章中的表述方式。以下引用《试验设计与分析》中的定义,同时也是重复DoE简介的内容,即试验是认识黑箱子的过程,通过控制输入(可控制变量),并观察输出(可观察变量),构建输入与输出之间的模型。
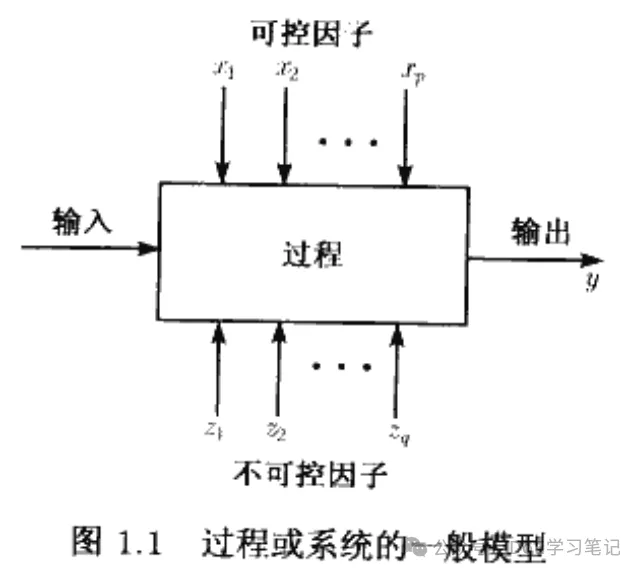
一般地,实验可以用来研究过程和系统的性能。过程或系统可以用图1.1所示的模型来表示。通常可以形象地将过程视为操作、机器、方法、人以及其他资源的一种组合,它把某种输入(通常是一种物质)转变为有一个或多个可观测的响应(response)变量的一种输出。某些过程变量和材料特性x1,x2,···,xp是可控制的,而另一些变量z1,z2,···,zq是不可控制的(尽管它们对试验的目的来说也许是可控的)。[1]
此处引用《试验设计与分析》中的一个两因子完全析因设计试验,之后基于该案例介绍相关术语。
一位工程师设计一种用在某装置内的电池,该装置将遭受温度忽高忽低的极端变化. 他这时能够选择的唯一设计参数就是电池的板极材料,有3种可能的选择。当安装好这种装置并送到现场去之后,这位工程师就再也不能控制这一装置所遇到的温度的极端变化了,经验告诉他,温度有可能影响电池的有效寿命. 但是,为了试验目的所需,在生产研制实验中,温度是可以控制的.
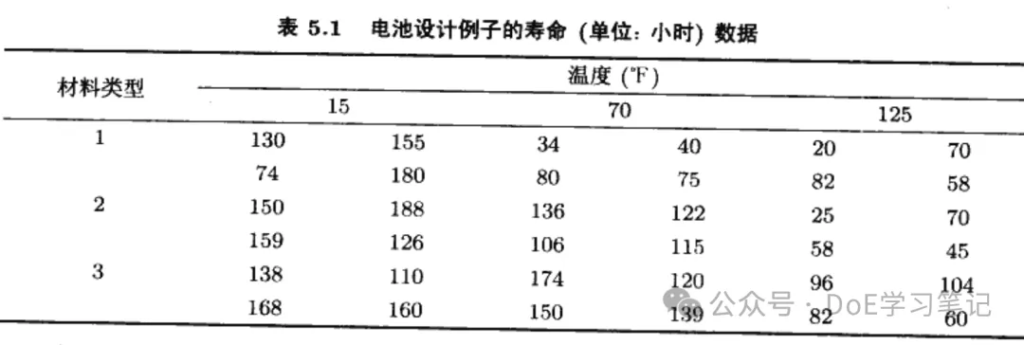
工程师决定在 3 个温度水平 (15 °F, 70°F和 125 °F) 上检验所有3种板极材料,这 3 种温度与产品使用的环境温度相符。因为有两个因子,每个因子有3个水平,所以该设计有时称为32析因设计。在每种板极材料与温度组合上检验 4 节电池,依随机次序进行所有 36 次检验。 实验和观测得到的电池寿命数据如表 5.1 所示。
试验单元、处理
试验单元是试验的基本单位,是接受处理的实体;处理是施加于试验单元的特定条件组合。
The experimental unit is the smallest division of the experimental material to which a single treatment is applied. The treatement is a specific combination of factor levels whose effect on the response variable is of interest. [1]
这两个概念看起来简单,比如针对Fisher开展的农田科学实验,试验单元就是最小单位的农田,而处理就是每块农田接受的试验条件组合(肥料,灌溉、农作物品种的一种条件组合)。
回到开篇的案例上,试验单元就是一种电池,而处理就是“板极材料和处理温度”的组合。
下面这句话,清楚表达了试验单元和处理之间的关系,试验设计时,避免两者之间存在依赖关系。
一个基本要点,同时也是始终隐含着的是,任何试验单元可以接受任何处理,并且对处理的分配均在实验者的控制之下。[2]
响应、因子、水平
响应就是试验定义中的输出变量或可观察变量,对应于案例中的“电池寿命”。
因子则是试验定义中的输入变量,既包括是可控的过程变量和材料特性,又包括不可控的噪声变量(有的噪声变量是生产时不可控,但试验时可控);因子对应于案例中的“板极材料”和“处理温度“。
因子又分为离散变量(discrete variable)和连续变量(continuous variable)。分别对应电池寿命案例中的“板极材料”和“处理温度”。
水平即因子的具体设置,比如三种板极材料类型,比如三个处理温度设定。在试验设计中,最常用的是编码化的-1和+1两个水平,比如处理温度15设为-1,125C设为+1,而其中心值70正好是编码化的0。
主效应、交互作用
主效应,即单一因子的效应,反映因子对响应的影响程度,也就是在高低两个水平下的响应变量的差异。
因子A的主效应=A高水平下的响应平均值-A低水平时的响应平均值。
对应电池寿命的案例,我们假定三个水平分别是低水平、中心点和高水平。忽略中心点数据,下图计算了每个条件下的四次重复的平均值。

温度的主效应= (230+342)/2 – (539+576)/2 = -271.5
材料类型的主效应=(576+342)/2 – (230+539)/2 = 74.5
交互作用,可以判断因子之间是否存在相互作用,是试验设计中一个非常重要的概念。
当因子B处于不同水平时,因子A的效应是固定不变的,则称A与B之间没有交互作用;如果因子A的效应依赖于因子B所处的水平,则称A与B之间有交互作用,此时因子B的效应同样也依赖于A所处的水平。换言之,A和B是对称关系。
交互作用是
结合电池寿命的案例,材料1时温度的主效应=230-539=-309,材料3时温度的主效应=342-576==-234;说明处理温度和板极材料之间存在交互作用。使用以下计算公式度量交互作用,同样满足A和B的对称关系。AB交互效应=(B处于高水平时A的效应-B处于低水平时A的效应)/2=BA交互作用=(A处于高水平时B的效应-A处于低水平时B的效应)/2
再将主效应的计算过程代入,交互作用可以被解释为表示设计矩形中两个对角响应平均值的差值。
结合电池寿命的案例,温度与板极材料的交互作用 = [(230+576)-(342+539)]/2=-37.5
至于交互作用是否显著,则要进行统计分析,此处不展开。
因子A的主效应给出了平均于其他因子的所有水平上的、A的不同水平之间的平均观测差异。A和B之间的两因子交互效应检查出平均于其余因子的所有水平上、B的不同水平处A的不同水平之间的差异是否相等,反之亦然。类似地,A、B和C之间的三因子交互效应显示出平均于其余因子的所有水平上,A和B之间的两因子交互效应在C的所有水平处是否具有相同的模式,或者等效地检查B和C之间的两因子交互效应在A的所有水平处是否具有相同的模式,等等。可以用相似的方式定义四个或更多个因子的交互效应,但很少有直接的实际重要性。[2]
模型、误差
一个良好的试验设计,会导出一个具有一定适应性的模型。最常用的模型是“效应模型”,模型中的因子系数,就是前面计算的主效应和交互作用的1/2(因为存在-1到+1的水平)。
科学和工程的大多数问题要求对系统的运行进行观测(observation)和实验,从而阐明系统运行的原因和方式。设计良好的实验常常可以导出系统运行的模型,这种由实验决定的模型称作经验模型(empirical model)。 [1]
误差反映的是统计的核心——波动,通过重复试验,我们可以计算出随机误差的大小,进而了解试验的精度。
随机误差是由试验中的不可控的变异而引起的,通常也是不可避免的;但是我们可以通过更精确的试验设计,比如识别更多的控制因子、区组化,进一步减小试验误差,这也是试验设计的精髓。
实验者无法控制的诸多变动(变异,波动)往往遮蔽了所观察的效应,而本书正是关于如何在这种情况下设计试验的。[2]
误差是统计分析的核心,也是判断主效应和交互作用是否显著的基础。具体方差分析(ANOVA)内容,此处不展开。
参考资料:
[1] 《试验设计与分析》
[2] 《试验设计》
[3] 德尔拓六西格玛培训资料