春节后学习公司内部的DOE培训资料,DOE(实验设计)的关键就是统计分析,而6-sigma的关键也是统计分析,所以最近一边看DOE培训资料,一边学习《六西格玛管理统计指南》蓝皮书。
在统计分析软件Mintab官网看到一篇很有趣的文章,举例介绍了DOE在企业中的应用,具体来说,是帮助企业对比两种原材料,是否会造成最终产品的口味变化,通过统计分析,分析数据,辅助决策。
为了加深理解,整理这篇文章的思路,并补充我的理解。
英文原文:
Creating the Ideal Guacamole: T-Tests for Food Manufacturers, Restaurants and Home Cooks
实验目的
avocado(鳄梨)好吃但是供应不足,价格上涨,厂家想知道,是否可以在guacamole(鳄梨酱)中添加少量的calabacitas替代部分鳄梨,目的当然是消费者可以接受(不会发现任何口味上的区别)。
However, with a loyal following, the manufacturer worried about changing the recipe and putting its brand at risk. The guacamole manufacturer decided to run a test and ask a sample group to taste and rank its “Classic” guacamole recipe versus its “New” recipe using avocados and calabacitas.
实验设计
第一步,收集数据;第二部,分析数据,进行对比(分析的本质是比较),具体使用的是T检验(T-test)。
The guacamole manufacturer gathers people to taste test, makes the two guacamoles to be ranked and starts collecting data, but without any statistical background, they turn to Minitab for help with their T-tests!
第一步:收集数据
两组样品,找25个测试者,尝试两种鳄梨酱,给出1~10的打分,其中10分代表味道最好。
To accurately compare the two product formulations, we asked 25 panelists to try both the Classic and New recipes and score taste on a 1-10 scale, where 10 has the best flavor.>
注意请测试者尝试两种鳄梨酱时,一定要随机!有的先尝鳄梨酱A,有的先尝试鳄梨酱B。“随机可以减少误差”(DOE的基本原则之一)
Knowing we needed to minimize bias, we randomized the order that our panelists tried the recipes so approximately half the group tried Classic first, while the other half tried New first.
这样就得到了25组数据,每组数据包括两个分值,分别对应两种鳄梨酱配方。
第二步:分析数据(Mintab方法,手动计算方法)
关键词:假设检验,t检验,配对t检验,
选择何种统计方法?
根据《六西格玛管理统计指南》,参数估计和假设检验是统计推断的两种重要方面。参数估计输出数值(比如100次投硬币,55次正面朝上,请问这枚硬币有问题的概率是多少?);假设检验输出判断,即产品是否合格,本文的两种水果是否等价。
这儿使用的当然就是“假设检验”(hypothesis test),假设检验的两条基本原则,一是反证法,二是小概率。具体的步骤这儿先不重复了。
假设检验根据总体的个数或样本的数量,又可以分为三类:单样本、双样本、多样本。 这儿的例子当然是一个双样本问题。【《六西格玛管理统计指南家》P100】
文章中有一个图片清晰的描述了这三类问题,见下图:
- 单样本:一个样本和理论值对比
- 双样本:两个样本之间的对比,成对t检验
- 多样本:多个样本之间的比较,ANOVA方差检验
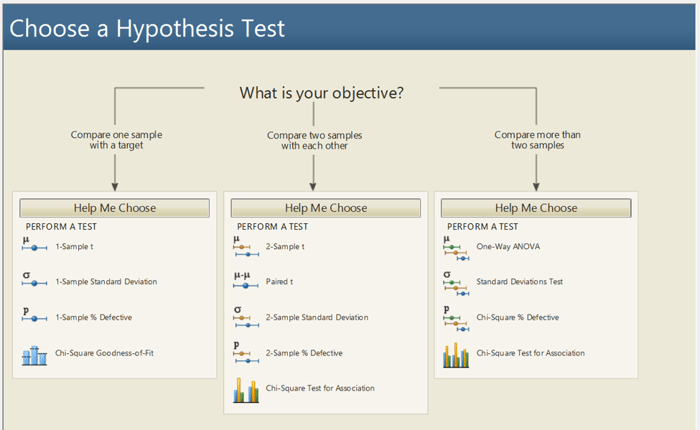
双样本问题,又分为多种情况,最常见的是双正态总体均值检验,根据“抽样的两组样本是独立的还是配对的”,又可以分成普通的检验和配对样本的检验。【《六西格玛管理统计指南》P128】
本文的问题当然是“配对均值检验”,原因如下:
Now we also know that each panelist tasted both recipes, so we want to compare the recipe means for a matched set items. The Paired t is the appropriate test here because it considers that the observations in the Classic and New columns are not independent, as each panelist scored both recipes.
为什么是t检验? 因为样本量是25个,不能简单的视为正态分布,而要使用“学生t分布”,只有当自由度超过30以后,t分布和正态分布的差别很小,此时完全可以用标准正态分布替代t分布。【《六西格玛管理统计指南》P78】
一般情况下,配对检验就是对于差值进行单总体的假设检验。 【P133】对于本文的例子,就是每个测试者对两种鳄梨酱的打分之差的均值进行检验,这就变成了均值是否为0的单样本检验问题,问题就变简单了。
具体统计结果
首先要强调假设检验五步骤中的最后关键步骤——如何判断检验结论,常见的三种方法如下: 【《六西格玛管理统计指南》P100】
- p值比较法 (p值的含义,何时推翻零假设,何时接受零假设?)
- 置信区间法 (计算出对应显著性水平比如95%下的置信区间,看是否包含零假设对应的参数值)
- 临界值法 (常见于手动计算,计算出对应置信度比如5%时,分布曲线上的临界Z值或t值,然后和实际值对比,看是否落在单侧或双侧的拒绝域)
对应到本文的例子,Mintab直接给出了统计分析结果,如下图所示。
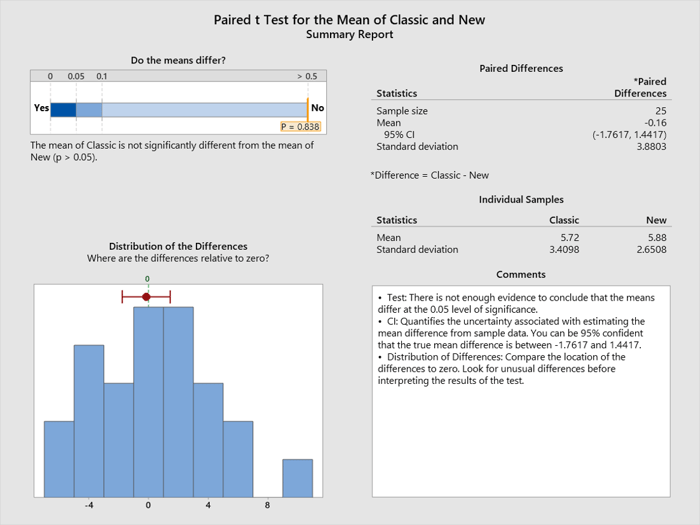
图中左上角是方法一的p值=0.838>0.05,“p值是因为随机得到零假设的概率“,远大于0.05(默认推翻零假设的临界值),所以”无法拒绝零假设“(不是”零假设成立“,注意两者的区别),即”两种鳄梨酱之间没有显著性差异“。 如果mintab计算出的p值<0.05,那我们就需要推翻零假设,接受“备则假设”(alternative hypothesis)。
图中左下图是差值(difference)的分布图,方法2的”置信区间“是(-1.7617,1.4417),包含零假设对应的默认值0,所以接受零假设。
右上角是具体的均值(mean)和标准差(standard、 deviation)。
Minitab calculates the differences for each row, with those differences are plotted in the histogram. The average difference is very close to zero (-0.16) and the red interval provides a range for the true mean difference, telling me that the two recipes are not different after all. This means my taste testers could not detect a difference between the recipes!
如果不用mintab软件,如何手动计算上图的数值(均值,标准差,p值)? 【这就是中国学生上课要学的方法三“临界值法”,可惜太多精力放在计算上,毕业之后就很容易把原理忘了,像我一样,还需要重学一遍啊。】
- 因为是配对t检验,所以直接计算每个测试者给出的差值
- 再计算差值的平均值(mean)是-0.16,差值的”样本标准差“是3.8803。【可以手动计算,可以用excel中的STDEV或STDEV.S函数,即“样本标准差“计算公式,而不能用总体标准差stdevpa或stdevp】
- 然后计算数值0对应的t值
- 这儿是双侧t检验,计算双侧总面积为0.05的临界t值,大于t的区域即为拒绝域。
- 对比0对应的t值与上面的临界t值,前者更大,落入拒绝域,拒绝零假设;后者更大,没有落入拒绝域,接受零假设。
抽样测试的“统计功效”——抽样量是否足够?
为什么要进行统计功效(Statistical power)分析?
《六西格玛管理统计指南》P101指出,假设检验中会出现两类错误:第一类错误是“拒真概率”,即零假设为真,却拒绝零假设的情况,这个概率就是显著性水平𝛂;第二类错误是“纳伪概率”,即备则假设为真(零假设为假),却拒绝备则假设的情况,这个概率是第二类错误𝛃。
第一类错误,是我们人为设定的,比如常见的0.05(显著),更宽松的0.1,或更严格的0.01(非常显著)。
根据下面的定义,统计功效(statistical powder)是1-𝛃!
抽样量越多,统计功效越强,25个抽样量,可以确保有87.1%的概率,识别出差异。如果抽样量太小,识别出差异的概率变小,难以作出更好的判断。
统计功效是什么
统计功效(英语:statistical power,又译统计考验力或统计检定力)在假设检验中是指当备择假设(H1)为真时正确地拒绝零假设(H0)的概率。
换言之,功效也可以看作是当备择假设为真时将其接受的概率。当功效增加时,第二类错误出现的概率(即假阴性率β)减少。此时,功效可以表示为(1-β)。
在给定的显著性水准下,功效分析可以用于计算给定效应值时所需的最小样本数;相反地,功效分析也可以用来计算给定样本数时所能检验到的最小效应值。
统计功效 – 维基百科,自由的百科全书
为什么评估统计功效
Before I get too excited about the results, I need to verify that my test had adequate power. Statistical power is the probability of detecting an effect, assuming it exists. I want to avoid the mistake of assuming there is no difference between the recipes based solely on the fact that I had a weak experiment. Minitab easily helps me out here by calculating the probability of detecting the practical difference between the recipes using Minitab's Diagnostic Report.
Given my sample size, I had an 87.1% chance of detecting the difference as shown below. This tells me that my test was not weak, meaning it had adequate power to detect a difference between the recipes.
我的补充
最近刚看完《六西格玛管理统计指南》(蓝皮书)P82 4.1 正态总体的抽样分布——4.1.2 “双样本均值差的分布”这一部分,所以这儿有一个问题:为什么不是“双样本均差的分布”。
如果我们直接对比以上两个抽样分布,那就是“双样本均值差”的分布问题,可以对比也可以,但是太麻烦,而且我猜猜波动会更大一些(待确认)。
因为在本试验中,每个测试者依次评估两种鳄梨酱的味道,就是上面所说的“not independent, as each panelist scored both recipes”,所以每个测试者直接给出一个确定的“味道差值”,所以我们直接分析“差值的分布”,而不用分析两个分布的差值,前者比后者更简单,因为前者是和理想值“0”做对比!
《统计学的世界》中的先加牛奶还是先加咖啡的例子,也是一个“配对样本”的例子。
这让我想起了之前看到一篇“老干妈”的报道,使用便宜的辣椒代替昂贵的辣椒,结果资深消费者感受到了“味道不正”,引起消费者的抱怨。
这不就是DOE(实验设计)和统计分析的用武之地嘛!
我们使用统计分析方法辅助科学决策,更换原材料同时避免影响消费者体验。
当然老干妈也可能知道口味又变化,更多迫于成本的压力吧。详情见下文
老干妈“变味”了?-瞭望智库
2020-03-28 1.5hour 第一篇统计分析的博文,以后结合阅读《六西格玛管理统计指南》阅读进度,补充我的理解和实践。
2020-03-05 更新本文,随着《六西格玛管理统计指南》的阅读,发现我有一些理解错误,大幅度更新本文,引用蓝皮书的内容,详细说明如何选择统计方法,判断结论的几种具体方法,以及统计功效的具体含义,终于借着这篇文章的案例,把相关知识理解透了!
2020-06-20 接着整理”抽样量和统计功效“的读书笔记,重读并简单更新本文,本文是统计功效的具体例子。那工作中有一个实验,只取两个样本进行比较,情况如何呢?