优秀的科学家通过构造实验获取新的知识,平庸的科学家往往会通过实验得到许多数据,但是无法获得新的知识。__《女士品茶》
DMAIC Improve阶段(最佳实践改进)和DMADV develop阶段,都有经典DoE部分,合并更新。
主要内容
- 实验设计基础
- 全因子设计
- 全因子分析和诠释(九步法)
- 部分因子设计
- 部分因子分析和诠释(九步法)
- POA爬坡设计
- RSM响应曲面
关键知识点:
- 使用全析因设计和高解析度部分析因设计,可以建立y和x的一阶模型,即线性模型; 如果加入中心点可以分析出是否模型弯曲(只做中心点实验,快速确认),如果存在弯曲,就补充新的实验点(比如CCC,CCI,CCF等),进而建立二阶模型。 这也是序贯实验的体现,不是直接做RSM
- 部分因子析因设计:最极端情况是只分析主效应,忽略二交互(此时解析度为III);如果因子没有那么多,推荐做法是考虑主效应和二交互,忽略三交互(解析度为IV,主效应与三交互混杂);更高解析度需要更多实验,没有必要,违背了筛选实验的初衷。
- 随机化你不能控制的因子,区组化你能控制的因子。 区组化的对象,同时是Design Expert软件中的HTC因子(hard to change);
- 为什么要做中心点实验:一是在线性模型(2水平实验)基础上,快速判断是否存在弯曲(模型是否是二级甚至更高阶);其次是判断实验的误差,最好是随机化多做几个中心点实验。
- 如果需要做转换,Minitab比较麻烦,Design Expert会更方便;
- 如果模型存在弯曲,说明线性模型不足以表征实际的数据规律,需要增加实验,变成RSM;增加二阶因子项甚至高阶因子项(一般只需要二阶)
- 如果模型存在拟合,原因就很多,之前讲课上经常强调的是过拟合(添加了太多无关紧要的因子),还可能欠拟合(遗漏了重要的因子,我感觉这个实际工作中更有可能发生),还可能数据太差(比如测试系统误差太大),等等;总而言之,拟合很差的话,原因有很多,要回到原点,分析DoE的意义,因子选择和范围是否合理等等。
- DoE分析和诠释:模型系数的方差分析,模型本身的方差分析,残差分析(残差四合一图)。 每一个都很重要
DoE中常见的几个误区:
- 做试验时,没有想好DOE的顶层设计——试验设计的目标是什么! 要解决什么问题,这到底是不是一个问题。(analysis筛选和验证root cause)
- 跳过”筛选实验“,直接进行优化实验,一开始就要建立y和x的传递函数。这样的坏处,可能陷入细节无法自拔,“螺蛳壳里做道场“,在不应该细化的范围细化研。
- DOE都停留在优化设计(优化实验)阶段,没有做到稳健设计(稳健实验);
- 对噪声因子的研究没有用稳健设计的思维去试验,比如UV 光强作为控制因子和噪声因子,会有不同的分析思路。
- 陷入工具迷思,使用一个大而全的DoE,从第一步做到最后一步。 我反而喜欢小而美的DoE,穿插简单对比实验,只在核心地方使用DoE。
- 想要一次做完DoE,指望一口吃成胖子。正确的做法时“第一次DOE不要投入超过25%的资源”。
next step:
- 在Design expert上重复案例分析
1. DOE实验设计基础
实验设计是什么:规划、实施和分析的方法,控制输入,观察和测量输出变化;用最有效的方法获得信息和规律。
实验设计是研究黑匣子的输入(因素)和输出(响应)的过程。
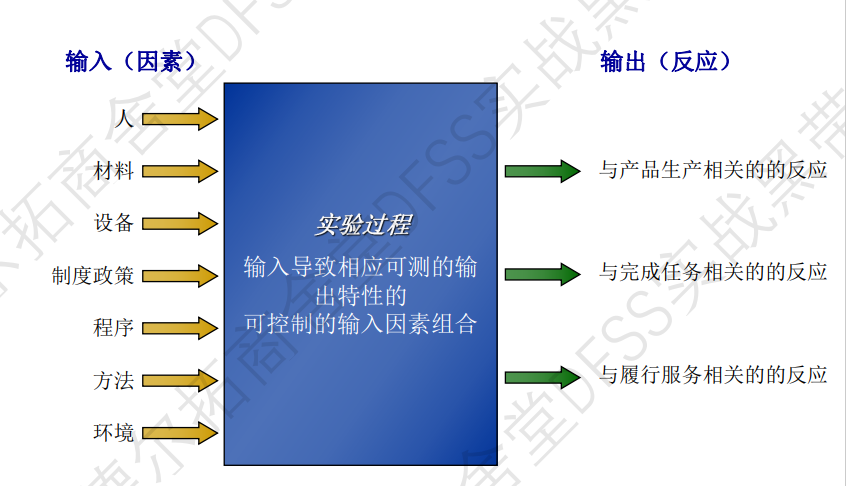
实验的四大基础目标:
- 筛选设计:确定显著的变量和交互作用,“从繁杂的多数中分离出关键的少数”
- 对比设计:单因素实验,一对标准,一对一和一对多的对比法。(假设检验的单因素实验)
- 优化设计:x取哪些水平,y可以达到最优解。
- 稳健设计:不仅y值达到目标,还要y抗干扰,对噪声不敏感。
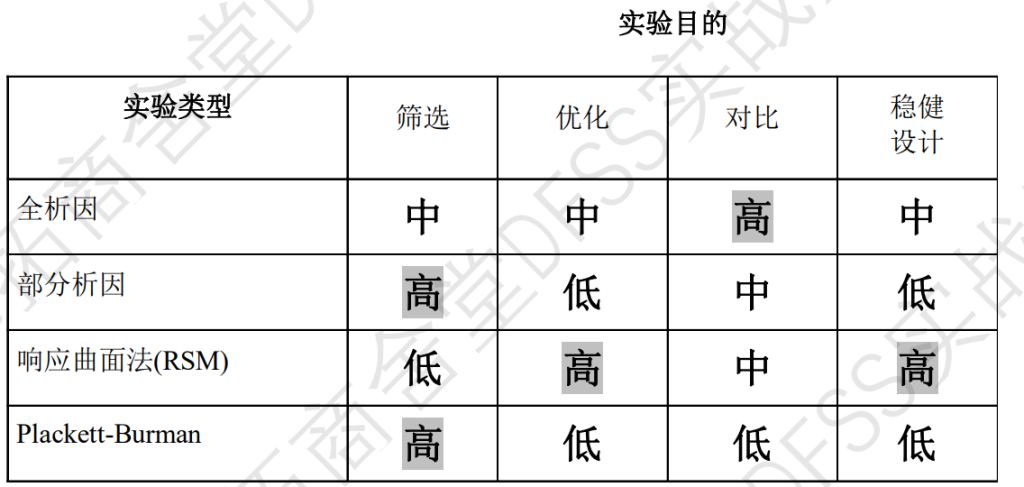
实验目的和具体的实验类型
- 筛选实验:常用部分因子析因实验和PB方法
- 优化设计:RSM(核心是得到y和x的传递函数,函数越精密越好,所以曲面响应一般要比线性的全析因法)
- 对比设计:全析因,不会牺牲掉交互作用。
- 稳健设计:RSM中的传递函数只是针对平均值,但不确定是否稳定,波动是否很大。
思考试验设计的统计学意义:x和y的变异从何而来,如何将y的变异最小化,如何使用假设检验和置信区间。
试验设计的迭代过程:提出设想,设计试验,收集数据,分析结果;优化设想,循环重复。(这就是《Mckinsey Mind》的question solving flow,设想就是hypothesis)
最简单的序贯设计:screen筛选设计——refine改进设计(建立一阶模型,研究最佳研究范围)——优化设计(建立优化模型,先加中心点实验,再考虑增加更多实验点)——确定模型预测(验证实验)

DoE中的关键概念,细节略
- 正交
- 运行顺序,标准顺序
- 模型
- 响应,因子,水平
- 析因实验
- 全因子,部分因子
- 随机化和区组化:随机化你不能控制的因子,区组化你能控制的因子!
- 实验误差
- 中心点
2. 全因子设计和九步法分析
关键词:
- 主效应,交互作用
- 残差分析
- 效应的帕累托图:对比效应和二交互作用的大小
- 统计学模型:系数和效应的关系
九步法分析:
- 查看数据:直觉分析(gut feeling)
- 拟合模型
- 简化模型(删除不显著的参数,p>0.1,不建议直接基于0.05删除)
- 残差分析(residual error)
- 是否需要转换(如果不正态,考虑Box-cox转换)
- 模型是否合格(模型分析:模型的残差,curvature,lack of fit,pure 而若人,F检验,根据p值分析是否显著)
- 选定模型
- 诠释模型(从机理上理解,把相关关系转换成因果关系)
- 执行新流程
模型参数的方差分析(ANOVA) – analysis of variance
- 查看main effect是否显著,再进一步确认哪些main effect显著
- 二交互,同上
模型的方差检验
- curvature 曲率:根据中心点实验,来判断模型是否需要二阶或更高阶因子项;如果p<0.05, 显著,存在弯曲; p> 0.05,不需要平方项,线性模型是ok的
- lack of fit失拟: 失去拟合,即模型不能很好的拟合实际数据的关系,实际原因有很多,比如存在弯曲(应该有二阶或更高阶因子项),比如DoE遗漏了一些重要变量(欠拟合),比如有太多无关的因子(过拟合),比如数据太差。 p> 0.05,说明没有失拟问天
- 模型的S(标准差),R-sq, R-sq(pred),R-sq(adj): pred接近于R-sq和adj,模型不存在过度拟合并具有足够的预测能力。(多么接近算ok?)
残差分析
- 残差:实际值与模型预测响应值之间的差值
- 为了验证回归模型的有效性,残差要符合以下假设:
- 是统计独立的(无相关性)
- 是正态分布的
- 源自一个稳定(受控)的总体
- 具有方差齐性.
- 为了验证这些假设,我们利用下列残差图(四合一残差图)进行分析:
- 1. 残差Vs.运行顺序(时间顺序)(右下图)
- 2. 残差Vs.预测响应值 (右上图)
- 3. 残差正态概率图. (左上图)
- 4. 残差vs.因子图. (左下图是直方图,下图没有残差-因子图)

3. 部分因子设计、分析和诠释
关键词:
- 筛选试验
- 混杂
- 解析度resolution: 推荐解析度为IV!所以使用下图的绿色和黄色运行次数,避免使用红色运行次数。
- 效应稀缺原理: 三交互及以上交互,都可以忽略。
- 设计生成元 (放弃)
何时使用部分因子设计进行筛选试验:存在大量因子(超过5个),找出显著性的变量,排除不显著的变量。Narrow down之后,再做全因子实验设计
筛选试验(部分因子设计)是序贯设计的起点。

3. 爬坡实验
放弃,我更愿意直接通过补充实验,或者新一轮DoE,把目标值cover进来,然后做优化实验。
4. RSM 响应曲面实验
何时做RSM:模型存在弯曲,也就是线性模型之后,增加中心点实验,发现模型存在弯曲(curvature,p<0.05).
如何做RSM: CCC,CCI,CCF,分别有不同的使用场景,比如CCC是外延,CCI是内缩。
5. 稳健实验
稳健Robust
不仅考虑响应值的均值,还考虑响应值的波动,特别是对噪声变量的变动。
稳健实验的目的是,降低噪声变量对响应值的影响。
首先要明确有什么噪声因子
- 固定参数的波动:比如机器设定速度4m/min,实际机器速度存在一个波动范围。
- 环境因素,比如温度湿度的波动
- 设备设定,比如设定值和实际值的差异
- 损耗:比如设备随时间而老化,测试基材随测试增加而波动增加,等等
- 等等,
稳健实验的响应值:信噪比
三种稳健设计方法:
- 田口设计
- 组合表法
- 多重响应法
稳健设计之降低变异的方法
- 脱敏:利用噪声变量和控制变量之间的交互作用,选择一个噪声变量干扰更小的控制变量的范围。(前提是存在一个可用的交互作用)
- 缓化:获得响应值和噪声变量的模型,然后计算“导函数”,计算导函数为零对应的参数设定值。
- 调优:寻找一个影响噪声变量的新变量,建立一个噪声变量和新变量的模型,使之最小。
2024-7-20 基于之前的草稿,整理发布;完成了一个小目标,重读并梳理一遍DMAIC的统计部分(精益部分暂略)
