主效应和交互作用是试验设计的一个非常重要的概念,在详细介绍可能的设计类型、统计分析之前,更彻底的理解是至关重要的。
从爱迪生到DoE:告别蛮力试验 介绍了试验设计的优势:DoE有更高的试验效率(更少的试验次数),最重要的是可以量化因子之间的交互作用,这是传统的盲猜法(最佳猜测法)和一次一因子法所欠缺的。
DoE基本术语 介绍了主效应和交互作用的定义和计算过程。
2024年下半年,我在部门内这样分享DoE的优势,但事后发现,这还远不能激发大家的兴趣。
交互作用的本质是什么?因子之间存在显著的交互作用,然后呢?这
就是本文要努力回答的问题。
一、交互作用的本质
理解交互作用(interaction)的关键是可加性(additive)。
考虑一个具有两因子A和B的试验,每个因子有4个水平。举个例子,可以将A的水平视为光固化胶带的四个光强条件,将B的水平视为光引发剂添加量;响应变量是胶带剥离强度。假定没有不可控的变异,获得如下表格的测试结果[2]

从表格中可以看出如下的规律:(a)对于B的所有水平和行平均值,A的任意两个水平对应的观测值之差均相等。例如,A从水平1到水平3时,响应加1;A从水平1到水平2时,响应加3。
(b)同理,对于A的所有水平和列平均值,B的任意两个水平的观测值之差均相等。条件(a)、(b)是相互等价的。如果符合以上的规律,我们就说因子A和因子B对观测的影响是可加的。
可加性的含义是,总响应的变化等于独立改变两个因子的单独变化之和。每个因子对观测值的独立影响,可以用每个因子的主效应来量化。即有:
观测的总变化=A变化的平均效应+B变化的平均效应;
备注:如果符合可加性,因子的主效应进而可以使用相应的行平均值或列平均值比较而来。例如,将A的水平2与水平1进行对比的主效应是15.25-12.25=3,以此类推。
基于可加性的定义,我们就很容易解释交互作用:如果因子A和B是可加的,我们就说因子A和B不存在交互作用;否则,我们就说A和B之间存在交互效应。
实际试验中必然存在不可控变异的干扰,要想判断交互作用是否存在,首先,可以用“交互作用图”定性判断,如下图所示,平行的红蓝两条线代表不存在交互作用,交叉越明显,代表交互作用越显著。其次,统计分析会计算因子和交互作用的显著性,给出更准确的p值信息。
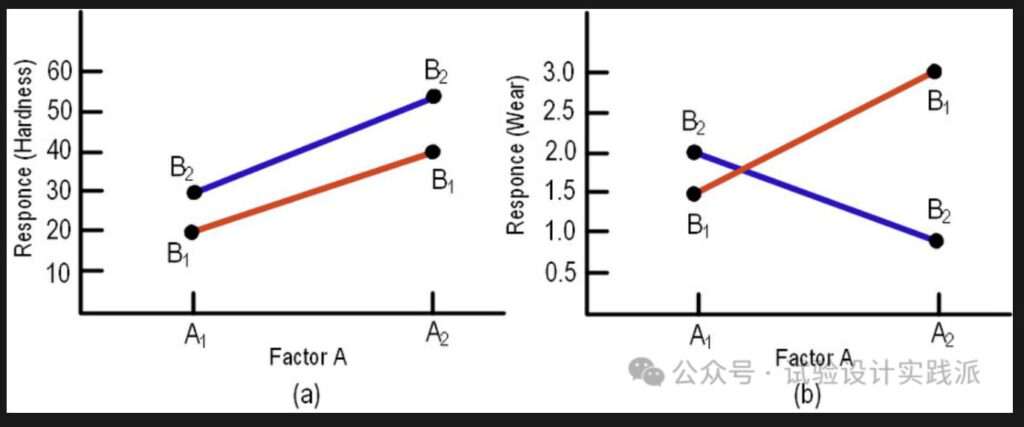
即使不考虑不可控变异的干扰,现实情况是,多数试验是不符合可加性原理的,换言之,因子间的交互作用是非常普遍的;这是“复杂系统”的非线性本质的体现,更是试验设计的价值所在。
当有交互作用时,为避免产生令人误解的结论,必须用析因设计。——《试验设计与分析》
二、第一性原理:探究交互作用背后的特殊含义
因为埃隆·马斯克而广为人知的第一性原理,强调从最基本的原理出发进行推理,而不是依赖类比或假设。
不论交互作用的统计分析结果是否显著,我们都要努力去理解实际发生的一切,理解该结论的物理意义,不能停留在显著与否(p值多少)这一个层次。
为什么要深究交互作用背后的特定意义?
首先,这有助于真正理解试验的控制机制,将输入和输出之间的模型推而广之,从一次的试验结论逐渐总结成更普遍的知识点。
(假定A和B存在显著的交互作用)交互效应的实际重要性在于,如果我们希望对B的水平提出技术建议,则有必要考虑A的哪个水平该出现。进一步地,除非交互效应的本质被充分理解了,否则将使用B的结论推广到试验中没有出现的A的水平上将是困难的。《试验设计》
其次,虽然假设检验中“拒绝是有说服力的,无法拒绝是没有说服力的”,但统计上有说服力,并不意味着“显著的交互作用一定具有真实意义”,一个典型的情况是,有的交互作用可以通过对观测值的变换消除掉。
所以,要努力从原理上解释那些显著的主效应和交互作用,特别是很多二交互作用甚至三交互作用都显著的情况,一定要小心。
[1] 《试验设计与分析》
[2] 《试验设计》
[3] Design of Experiment Methods in Manufacturing: Basics and Practical Applications, January 2012, DOI: 10.1007/978-3-642-25859-6_1
欢迎关注,一起学习成长~