根据《原因与结果的经济学》的“证据金字塔”,回归分析是证据程度最弱的工具,观察实验和准实验、随机对照实验,证据能力依次增强。其次在实际工作中,主要通过设计对比实验进行因果推理,相比之下,社会科学因为经常无法设计实验,会更多使用回归分析。
所以我不想花太多时间深入回归分析的所有细节,重点是模型检验和残差分析,弄清楚拟合模型的统计量的具体含义,因为在后面的DOE中会频繁使用。
核心内容:散点图和相关性,简单线性回归,模型检验、残差检验。
前提:何时使用相关性和回归分析,要求x和y都是连续型数据。当然更多是事后分析时用回归分析,事前能实验设计,就直接用DOE等工具。

第一部分:相关性,散点图
相关关系不等于因果关系。
使用相关性分析,确定x和y之间存在统计意义的相关性后,需要进一步解释其可能的因果关系。
具体分析工具:散点图,相关性系数(r)
Minitab相关性分析:
- 散点图: graph – scatterplot (两个变量之间的相关性分析)
- 矩阵图:graph – matrix plots (多个变量之间的相关性分析)
《原因和结果的经济学》中,提到“判断两个变量属于因果关系还是相关关系时,先回答三个问题”,排除是否存在时间先后、第三变量、逆向因果的可能。
第二部分:简单线性回归分析 P17-P62
只有一个x,对应“简单线性回归”,模型为 y = a +b*x + 误差,即直线方程; 多个x,对应“多项线性回归”
模型拟合的原理:最小二乘法,确定垂直距离平方最小的直线,即为最小二乘法回归线,此时的误差即SSerror最小。
残差Residual的定义: the difference or deviation between an actual observed value and the predicted value from the regression equation.
模型的三种误差:分类、量化表征
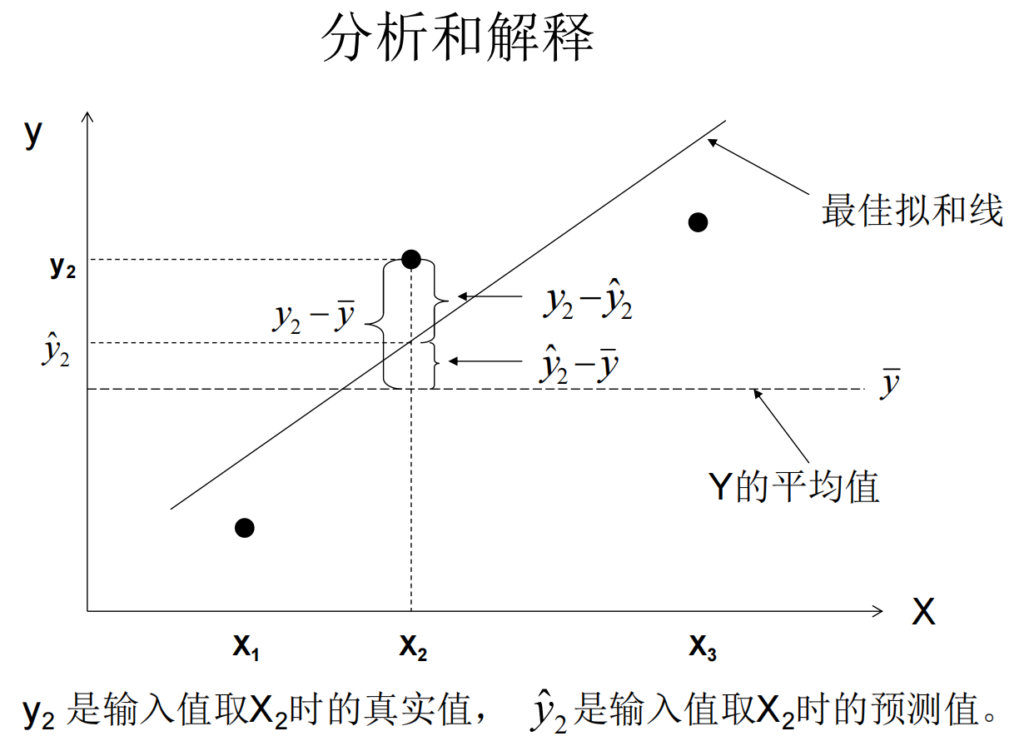
简单线性回归模型的“三种误差”: (所以在模型分析中,需要计算模型的纯误差、拟合优度(表征失拟误差))
- 由于不可控因素产生的重复误差或“纯误差”,简写PE,pure error
- 对输入变量x拟合不良而产生的误差,简写LOF,lack of fit,即“失拟误差“
- 测量误差,简写MSA
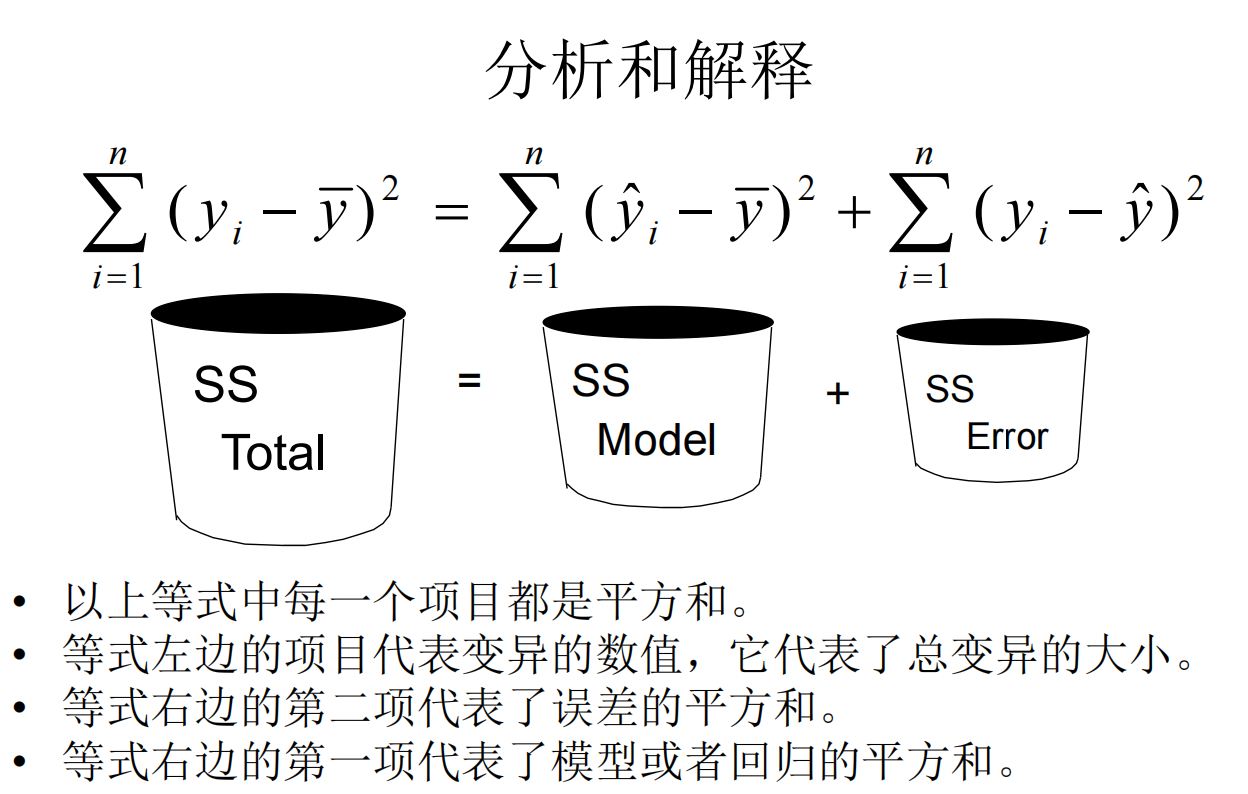
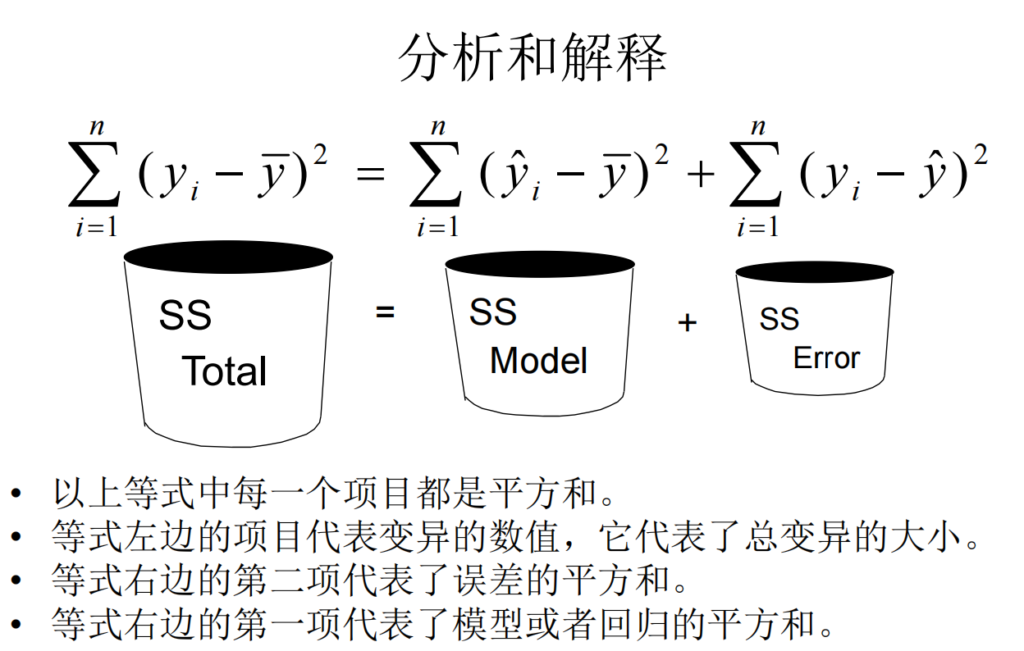
SST = SSM + SSE
总误差 平方和 = 模型误差 平方和 + 误差 平方和
三个误差的含义是什么?
- SST,或SS total:总误差,总变异量, 模型的SS total/ (n-1)就是方差,再开根号就是标准差。
- SSM,SS regression = SS model:
模型误差=拟合误差=失拟误差,模型预测值相对于平均值的变异量,反映了模型对数据变化的解释能力。 - SS residual error:残差,实际值和预测值之间的差异,也就是模型无法解释的变异量; (我自己的理解,包括了上面说的Pure error和测量系统误差)
具体如何做回归分析,下图的统计量的具体含义

1、模型系数是否显著:t检验
Coef是系数,计算原理是最小二乘法。
SE Coef 是系数的标准误(Standard Error of the Coefficient), 如何计算?
T是t统计量, T=Coef/ SE Coef
t检验,计算出p值;p<0.05,代表该系数显著。
- 系数的标准误 是指系数估计值的标准差,它反映了系数估计值的精度。
- 标准误越小,表示系数估计值越精确,反之亦然。
- 系数的标准误可以用来计算系数的置信区间,以及进行假设检验。
2、回归方程的标准差S,拟合优度R-sq,R-sq(adj)
S是回归方程的标准差,是MS error的开根号,MS error是均方,是SS error/DF error,所以S反映的是回归方程的纯误差的大小?
R-sq = SS model / SS total = SSM/SST
使用R-Sq (R^2)评估回归模型的拟合优度;R-sq越大,代表模型的预测能力越好,误差越小。
使用R-sq(adj)避免参数过多导致的过度拟合(模型项数p越多,根据以下计算公式,R-sq(adj)越小,可能会出现负数)

R-sq和R-sq(adj)的接近程度,说明模型的拟合好坏
R-sq (adj)一般要求大于80%,最小64%,代表拟合的好坏。
3、回归的ANOVA(analysis of variance):F检验
只看回归模型总体的变异,不细分其中的系数
DF, SS, MS, F, P : 这一部分是做变异的F检验分析,分析变异主要来自于模型还是纯误差,DF是自由度,SS是变异,MS是均方,MS error=SSerror/DFerror
不直接比较SS,而是比较均方MS
F在这儿代表“信噪比”大小,如下所示,p<0.05,回归模型具有统计上的显著性 (输出响应Y在统计上依赖X)

残差检验及其他
如果要应用方程,就必须做模型检验,残差检验是最主要的模型检验方法。
为什么要做残差检验???可能的模型问题是什么???
残差的四个假设:
- 独立的(无相关性)——>残差和实验顺序的关系图 (独立性检验)
- 正态的——> 残差的正态图,直方图
- 稳定性,即来自一个稳定(受控)的总体——>
- 方差齐性,即具有相等的总体方差——>


四种残差图:
残差图的解释及其应用



四合一残差图
- 左上:正态图,没有远离拟合线的异常点
- 左下:直方图,是否有异常的残差值,代表异常点;看模型是否稳定。
- 右上:残差与拟合图,分析方差齐性,不应该出现弯曲、漏斗等形状,而要均匀上下分布;
- 右下:顺序图, 分析随机性和独立性, 不应该出现明显的趋势
多元线性回归
多个x,多重共线性,方差膨胀因子(VIF), 这一部分略。
一般线性模型(GLM)
GLM的x,既可以离散,又可以线性; 内容略。
第四部分:逻辑回归
逻辑回归:x是连续型变量,y是离散型变量。
提醒:尽可能通过优化测量系统,将离散型变量y,转换成连续型和计量行数据。 尽可能不用逻辑回归。内容略。
2024-7-5 重读,整理; 2024-7-6 重读一遍,发布